V praxi se dnes standardně využívají pro posouzení oblastí diskontinuit železobetonových a předpjatých konstrukcí metody příhradové analogie a tlakových polí. Compatible stress field method (CSFM) vznikla rozšířením těchto klasických teorií, umožňuje vysokou míru automatizace a je v souladu s návrhovou normou. Metoda i přes svou jednoduchost poskytuje velmi realistický popis odezvy betonové konstrukce, a to jak v mezním stavu únosnosti, tak v mezním stavu použitelnosti.
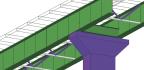
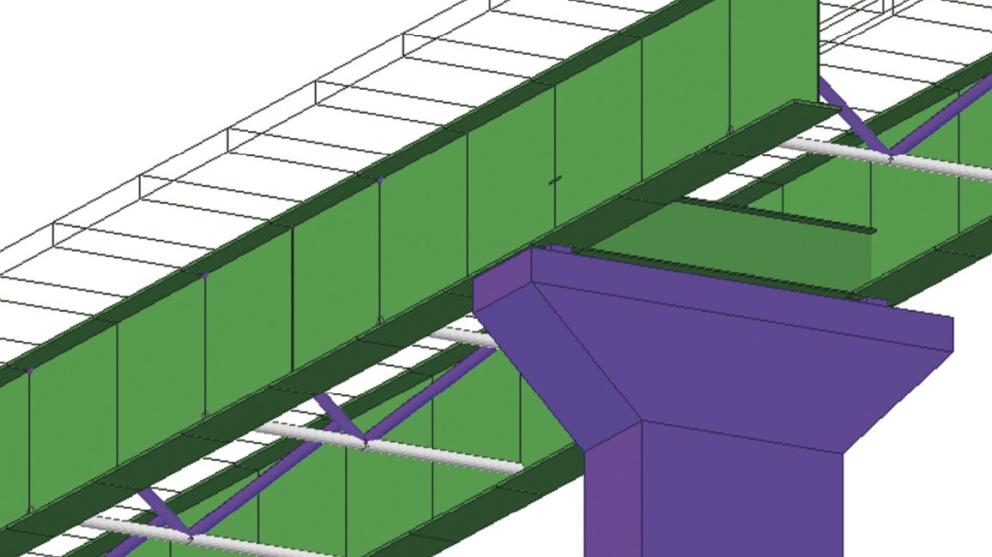
Standardní postupy pro navrhování průřezů betonových konstrukcí jsou použitelné v částech, kde platí tzv. Bernoulliho-Navieriho hypotéza o zachování rovinnosti průřezu po přetvoření (oblasti B). Místa, kde hypotéza neplatí, se nazývají oblasti diskontinuit (oblasti D). Patří sem části konstrukcí, kde působí soustředěné zatížení, kde dochází k náhlé změně průřezu, otvory atd. Z oblasti mostního stavitelství jsou to pak např. hlavice pilířů, nadpodporové příčníky, deviátory atd.
Modely náhradní příhradoviny
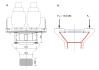
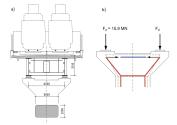
V současnosti se pro dimenzování D-oblastí nejčastěji používají modely náhradní příhradoviny (Strut-and-Tie nebo SaT) a tlakových polí (Stress Fields). Základním předpokladem při tvorbě SaT modelu je skutečnost, že pevnost betonu v tahu je zanedbatelná. Jednoduchý příhradový model chování D-oblasti v mezním stavu únosnosti je pak sestaven z prvků působících v tlaku a v tahu. Příklad typické D oblasti zhlaví mostního pilíře je uveden na obr. 1 a 2. V principu se nejedná o složitou úlohu a definovat základní SaT model s jedním hlavním příčným táhlem (obr. 2b) by neměl být pro mostního inženýra problém. I pro tuto základní úlohu však správné posouzení modelu v souladu s návrhovou normou může být zdlouhavý, manuální a iterační proces.
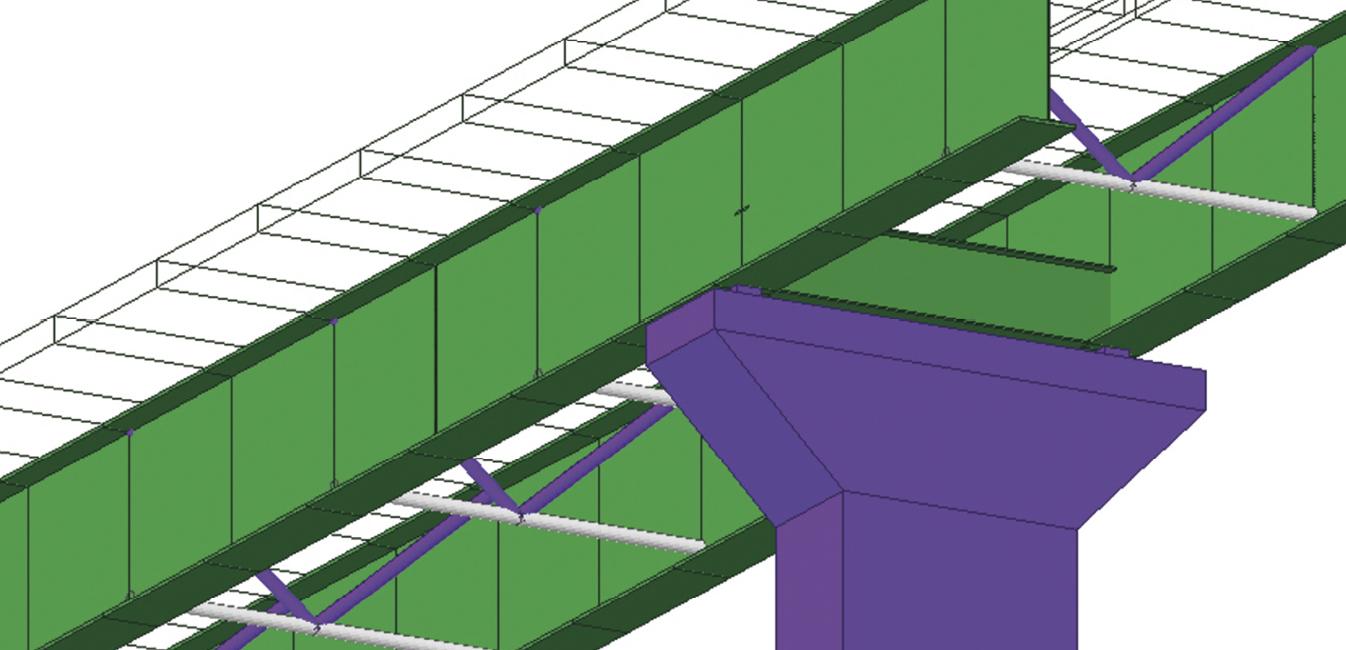
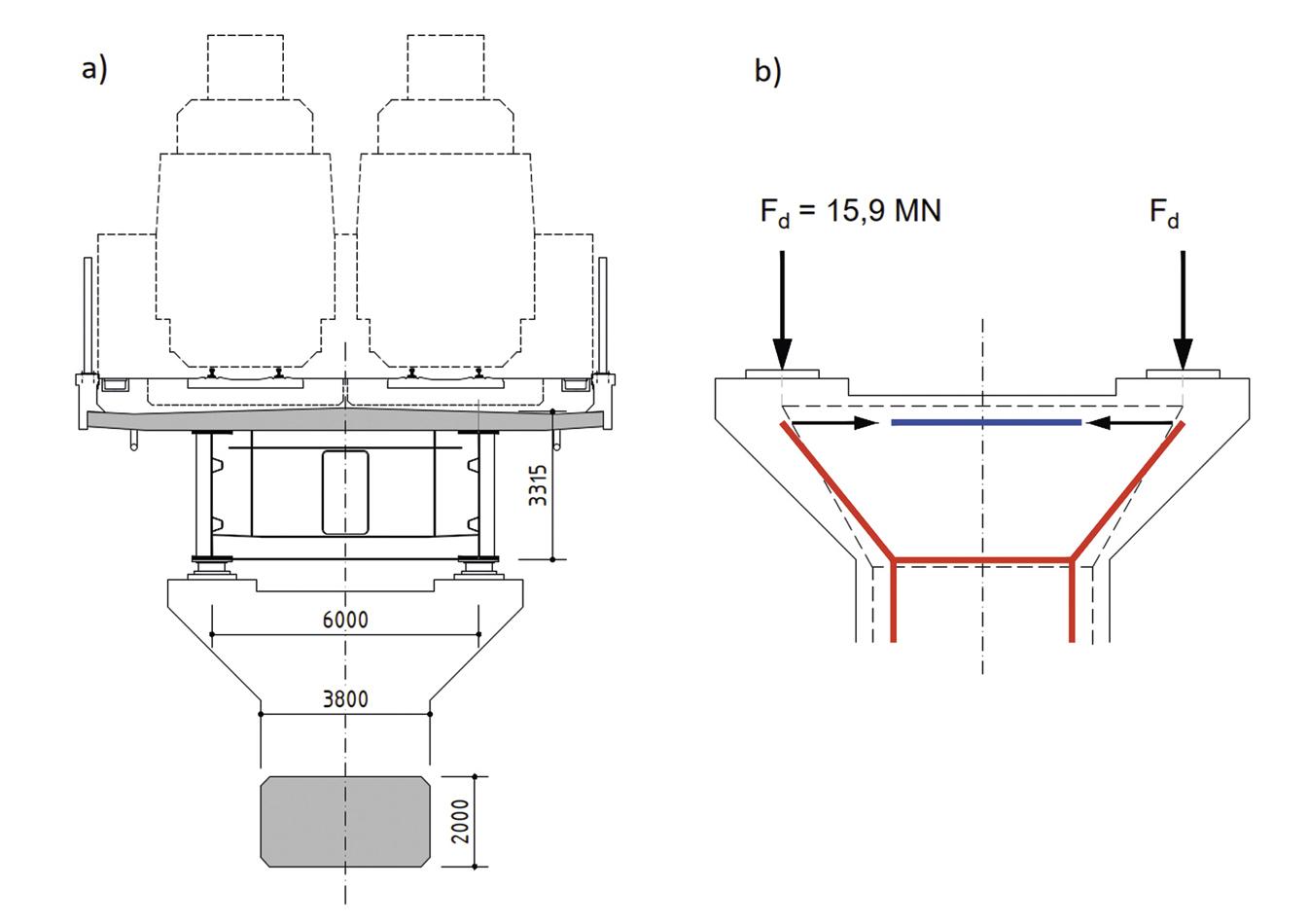
a) příčný řez v místě pilíře; b) náhradní příhradovina.
Je potřeba posoudit táhla, uzlové oblasti, příčné tahy v tlakových diagonálách atd. A pokud model nevyhoví, je třeba zvolit novou geometrii příhradoviny. Což velmi často vede k tomu, že statik si pouze jednou zvolí geometrii SaT modelu a posoudí jen táhlo z betonářské výztuže. Může se tak dopustit podstatné chyby. Pro ilustraci je na obr. 2b) čárkovaně uvedena alternativní příhradovina s „odvážnější“ geometrií. V případě dvou naznačených příhradovin vede rozdíl ve sklonu šikmé vzpěry k rozdílu 30% síly v příčném táhle. Volba příhradového modelu je vždy věcí zkušenosti a u složitějších konstrukčních detailů nemusí být volba příhrady, která bude dostatečně odpovídat skutečnému chování konstrukce, tak snadná jako u našeho příkladu. Příhradová analogie je také metoda pouze pro posouzení mezních stavů únosnosti a neumožňuje provést posouzení mezních stavů použitelnosti (deformace, trhliny), což jsou zejména v mostním stavitelství rozhodující kritéria, protože mají přímý dopad na životnost konstrukce.
Compatible Stress Field Method – CSFM
CSFM je moderní nelineární metoda pro analýzu D-oblastí a prvků, jejichž působení lze zjednodušit na rovinnou napjatost, tedy 2D model. Stále se ale vychází ze základního a bezpečného předpokladu norem: beton v tahu nepůsobí a veškeré tahy musí přenést výztuž. Compatible Stress Field Method (CSFM) je evolucí metod příhradové analogie a tlakových polí, přičemž odstraňuje jejich hlavní, výše zmíněné nevýhody: nejistoty ve volbě modelu, obtížnou automatizovatelnost a nemožnost posoudit mezní stavy použitelnosti.
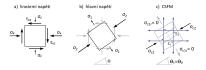
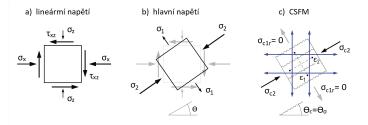
Cílem tohoto příspěvku je vysvětlit podstatu CSFM i za cenu dílčích zjednodušení. Princip CSFM lze vysvětlit na napjatosti základního rovinného elementu železobetonové konstrukce. Na obr. 3a je napjatost elementu, jak ji známe ze všech učebnic pružnosti a pevnosti. Pro případ našeho zhlaví to je např. napjatost v jednom bodě konstrukce, získaná například lineární, pružnou analýzou pomocí metody konečných prvků (MKP). Na element působí horizontální příčný tlak σx, vertikální příčný tlak σy a smykové napětí τxy. Z těchto napětí lze stanovit tzv. hlavní napětí a jejich sklon θ (obr. 3b). Element je pak namáhán hlavním tahovým napětím σ1 a hlavním tlakovým napětím σ2.
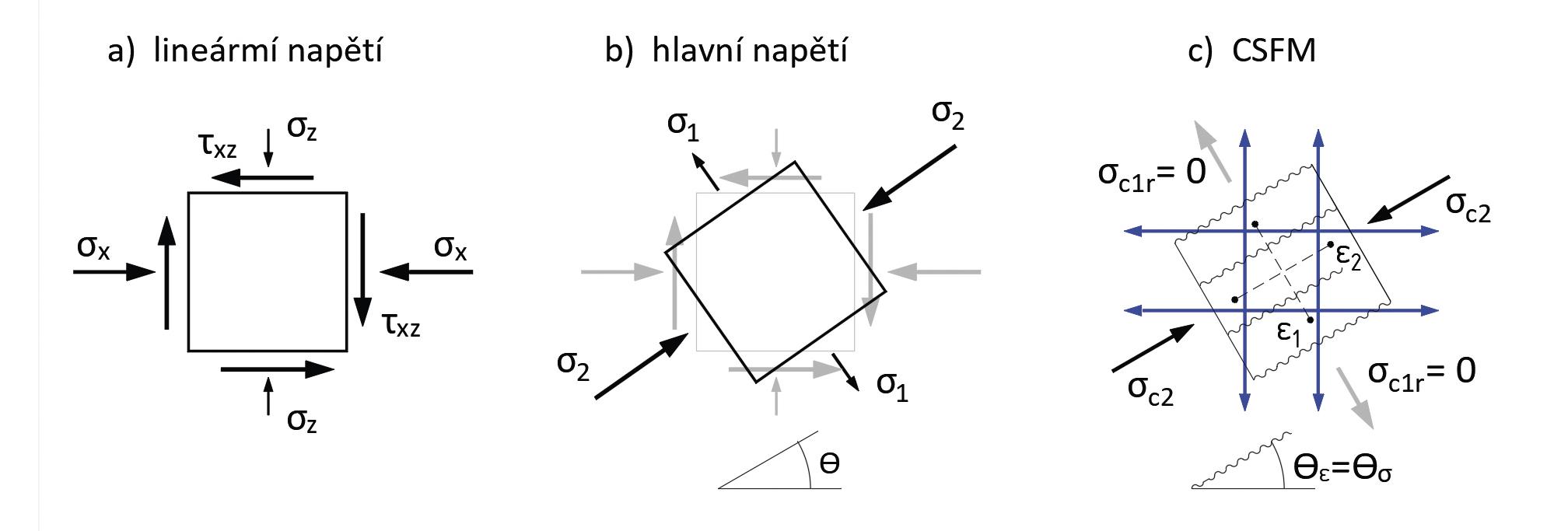
Obr. 3 – Princip CSFM: a) lineární, pružné napětí rovinného elementu; b) hlavní napětí; c) napětí při řešení pomocí CSFM.
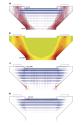
Jak bude vypadat napjatost stejného elementu analyzovaného pomocí CSFM? Napjatost je znázorněna na obrázku 3c. Ve směru hlavních tlakových napětí σ2 působí tlačený beton a vznikne tlakové pole s napětím σc2. Jak již bylo zmíněno výše, základním předpokladem je, že beton v tahu nepůsobí. Příčná hlavní tahová napětí σ1 tedy beton nepřenese, kolmo na jejich směr vznikne trhlina. Napětí σc1r tedy musí být rovno nule. Aby nedošlo k rozpadu našeho 2D elementu, musí veškerá tahová napětí přenést výztuž (naznačena modře na obr. 3c), která musí být součástí výpočtového modelu. Provede-li se tato analýza napjatosti pomocí CSFM spojitě po celé řešené 2D oblasti, je výsledkem spojité tlakové pole a pole tlakových a tahových napětí ve výztuži. Zjednodušená grafická reprezentace CSFM napěťového pole pro zhlaví našeho pilíře je uvedena na obrázku 7a. Kromě míry využití betonu a výztuže jsou na obrázku naznačeny také po oblasti měnící se směry vypočtených tlakových napětí σc2.
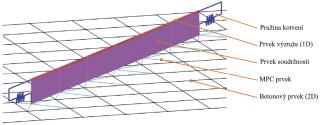
Analýza detailu nebo konstrukce pomocí CSFM je založena na metodě konečných prvků. Beton je modelovaný pomocí 2D stěnového elementu a výztuž pomocí 1D prutových prvků (obr. 6). Analýza se neprovádí v jednom kroku, ale je zřejmé, že se jedná o nelineární úlohu (beton v tahu nepůsobí). Zatížení se během výpočtu aplikuje po přírůstcích a řešení nelineárního systému rovnic se hledá pomocí Newton-Raphsonovy metody. Fiktivní rozetřené trhliny (ε1 je průměrná hodnota) se „tvoří“ kolmo na směr hlavních tahů, který se může během nelineárního výpočtu měnit, jak se element „postupně potrhává“ od jednotlivých přírůstků zatížení. Jinými slovy shrnuto, v CSFM se uvažuje fiktivní beznapěťová rotující trhlina. Výsledkem MKP řešení pomocí CSFM je kompatibilní napěťové pole (tzn. beton se v modelu nerozpadá na jednotlivé samostatně působící vzpěry) a pole poměrných přetvoření, která jsou spojitá po celé řešené 2D oblasti. To je velká výhoda oproti klasickým SaT přístupům a umožňuje to automatizovat a zpřesnit výpočetní model, jak bude popsáno v následující odstavcích.
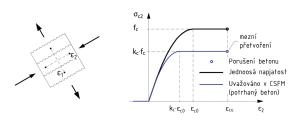
Jednoduchá formulace CSFM umožňuje použít standardní jednoosý parabolicko-rektangulární pracovní diagram pro beton v tlaku z návrhové normy. Jak je známo, tlaková pevnost betonu klesá, pokud je beton porušený příčnými tahovými trhlinami (obr. 4). Tento efekt tzv. tlakového změkčení (compression softening) je v metodě zahrnut automatickým zohledněním tzv. efektivní tlakové pevnosti betonu. Na základě úrovně příčných tahových přetvoření ε1 se stanoví redukční faktor kc a upraví se pracovní diagram betonu (obr. 4). Díky tomu, že je známo pole poměrných přetvoření po celé konstrukci, může být efektivní pevnost betonu v tlaku vypočítána automaticky v jednotlivých částech v závislosti na místní úrovni příčných tahových přetvoření ε1.
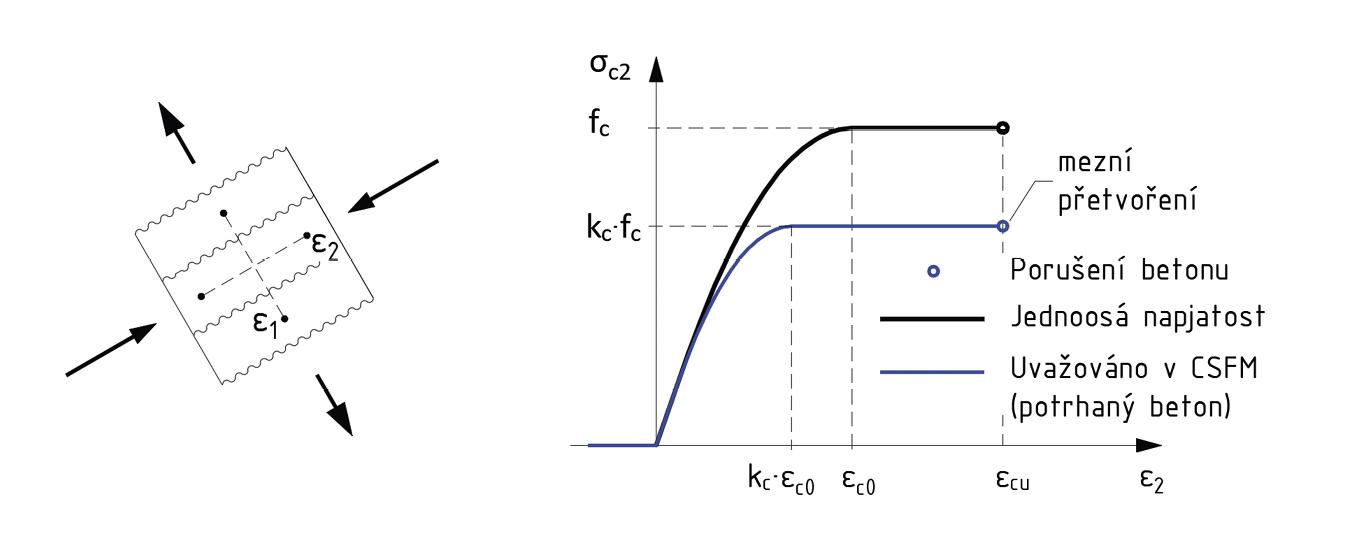
Obr. 4 – Pracovní diagram betonu se zohledněním limitního napětí vlivem příčných tahů (tlakové změkčení, pro ε1 > 0 a ε2 < 0).
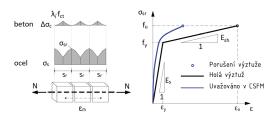
Dále se v CSFM uvažuje ztužující účinek taženého betonu mezi trhlinami na výztuž – tahové zpevnění (tension stiffening). Ve výpočtovém modelu se pracuje s průměrným poměrným přetvořením výztuže εm a upravuje se pracovní diagram výztuže (obr. 5). To umožňuje realisticky vystihnout tuhost železobetonové konstrukce porušené trhlinami. Stále však platí, že pevnost betonu v tahu se nepodílí na únosnosti. Pro posouzení je rozhodující maximální napětí ve výztuži σsr v trhlinách (obr. 5).

Obr. 5 – Pracovní diagram výztuže a diagram se zohledněním průměrných poměrných přetvoření výztuže s vlivem tahového zpevnění.
CSFM používá běžné jednoosé materiálové modely (pracovní diagramy), které jsou definované v návrhových normách. Pro posouzení MSU se potom používá standardní normový formát spolehlivosti – metoda dílčích součinitelů spolehlivosti. Metoda je tak díky své jednoduchosti vhodná pro inženýrskou praxi a je v souladu s návrhovou normou. I když se jedná o nelineární MKP analýzu, nemusí statik do výpočtu zadávat dodatečné materiálové vlastnosti a charakteristiky betonu, které ve stadiu návrhu ani nemůže mít k dispozici a které jsou nutné např. pro MKP nelineární analýzy založené na lomové mechanice. Jak již bylo naznačeno, velkou výhodou analýzy pomocí CSFM je kromě mezních stavů únosnosti rovněž schopnost posoudit mezní stavy použitelnosti: průhyby, omezení napětí a zejména šířka trhlin.
MKP model v CSFM je sestaven z několika typů konečných prvků (obr 6.):
- 1-D prvek s osovou tuhostí modelující výztuž.
- 2-D izoparametrický prvek modelující beton.
- Koncové pružiny pro model kotvení výztuže s koncovou úpravou.
- Speciální 2D prvek pro model soudržnosti mezi výztuží a betonem.
- Tuhé a interpolační vazby (Multi-Point Constraints, MPC) mezi prvky soudržnosti a betonem.
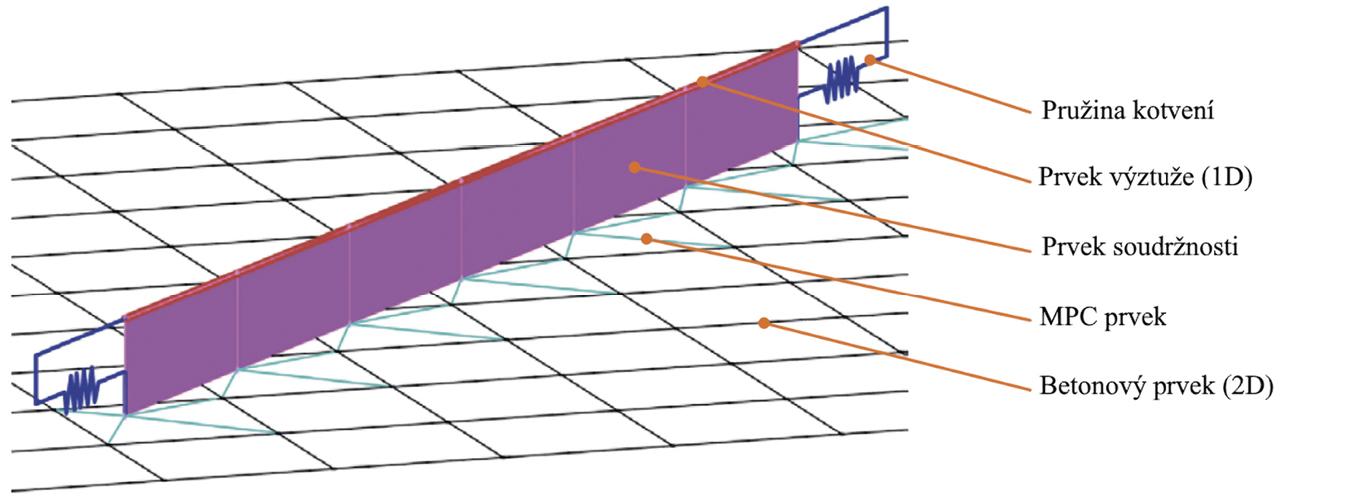
Obr. 6 – MKP model: konečné prvky výztuže připojené k síti betonových prvků pomocí MPC vazeb a koncových prvků.
Pokud navržená výztuž zabraňuje křehkému porušení prvku, bylo prokázáno, že CSFM dává navzdory jednoduchosti formulace velmi dobré předpovědi odezvy a mezní únosnosti konstrukce. Jinými slovy metoda není vhodná např. pro posouzení nosníků bez příčné smykové výztuže, které vykazují potenciálně křehké chování. Verifikace metody včetně experimentů jsou uvedeny v [1]. Podrobnější popis metody je nad rámec příspěvku a lze ho rovněž nalézt v [1].
Je zřejmé, že principy CSFM jsou obecné a její použití tak není omezeno jen na D-oblasti, ale lze ji využít pro modelování celých prvků nebo např. prefa dílců a tam, kde lze prvek zjednodušit na rovinný 2D model. Metoda a její implementace v softwaru byly také rozšířeny o možnost zadat předem a dodatečně předpjatou výztuž.
Příklad posouzení zhlaví pilíře
 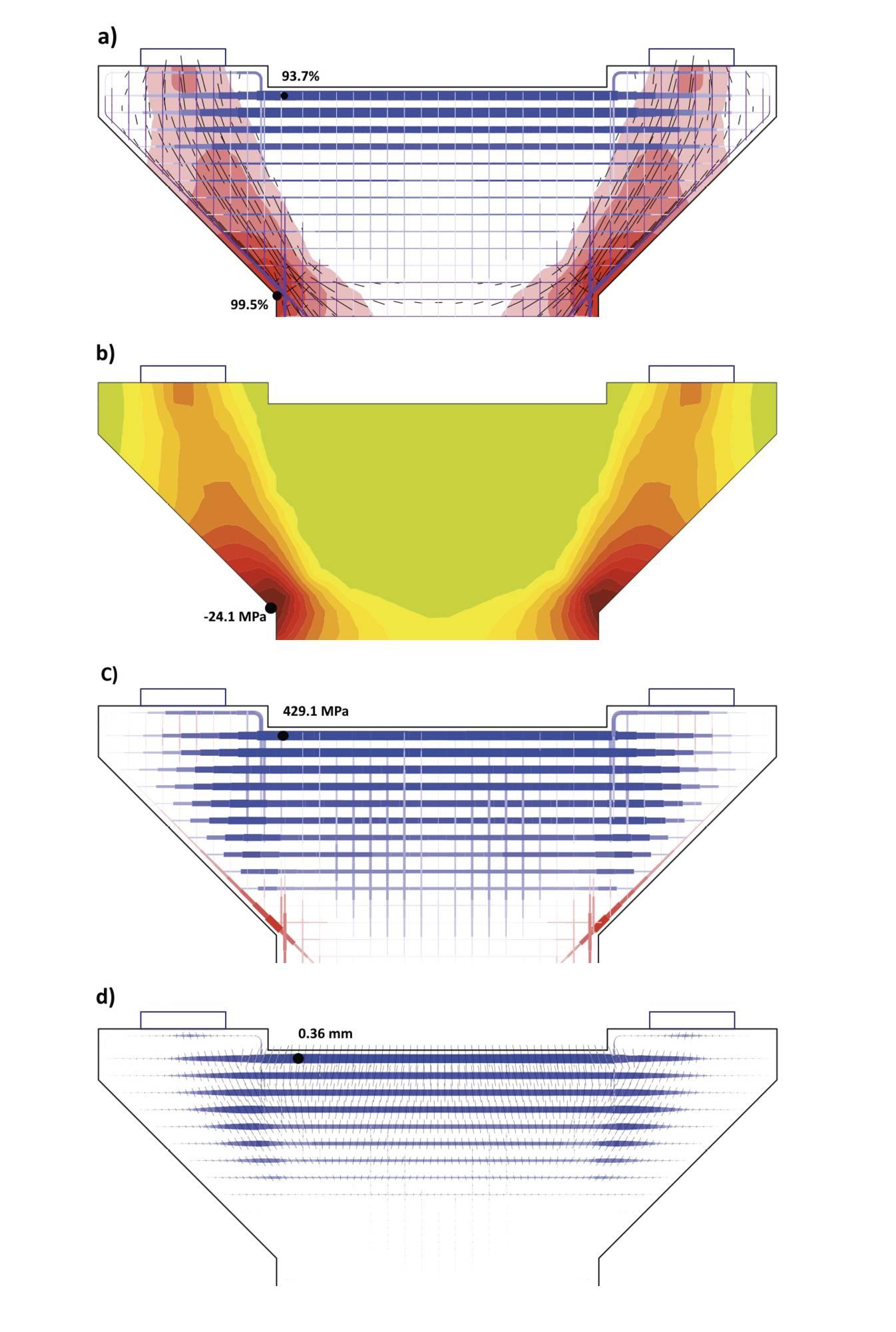 |
|
Obr. 7 – Hlavice pilíře: |
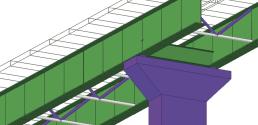
Praktické využití metody CSFM je ukázáno na posouzení hlavice mostního pilíře z obrázku 1. Jedná se o pilíř spojitého mostu o třech polích s rozpětími 30, 42 a 30 m. Hlavice ŽB pilíře je navržena z betonu C40/50, její tloušťka (v podélném směru mostu) je 2,0 m.
V horní části hlavice pilíře bylo nejprve navrženo příčné táhlo z výztuže B500 20 × ∅28 + 20 × ∅25 – horní čtyři vrstvy. Na obrázku 7a je uvedeno souhrnné posouzení v mezním stavu únosnosti se zobrazením tlakových napětí v betonu, směry tlakových napětí a využití výztuže. Detailnější průběhy napětí v betonu a ve výztuži jsou potom dokumentovány na obrázcích 7b a 7c. Výztuž příčného táhla je těsně pod mezí kluzu, rovněž napětí v betonu (a poměrná přetvoření) jsou v MSÚ vyhovující. Z výsledku výpočtu šířky trhlin (obr. 7d) je však zřejmé, že v MSP návrh nevyhovuje: wmax = 0,36 mm > wlim = 0,3 mm. Pro splnění mezní šířky trhlin je nutné zvětšit výztuž příčného táhla na 20 × ∅32 + 20 × ∅28. V případě wlim = 0,2 mm (např. pilíř v blízkosti pozemní komunikace generující slanou mlhu, stupeň vlivu prostředí XF2) by bylo nutné výztuž příčného táhla zvýšit dokonce na 24 × ∅32 + 24 × ∅28.
Závěr
CSFM je vhodná pro inženýrskou praxi díky tomu, že využívá jednoduché materiálové modely definované v návrhové normě. Umožňuje vedle mezních stavů únosnosti rovněž provádět posouzení mezních stavů použitelnosti, což bylo dříve např. s použitím SaT modelů těžko představitelné. Díky implementaci metody v programu IDEAStatiCa Detail je pak možné realisticky postihnout odezvu konstrukce a navrhovat a posuzovat oblasti diskontinuit, ale i větší celky efektivně a bezpečně.
CSFM byla vyvinuta zejména díky práci profesora Waltera Kaufmanna, vedoucího Chair of Structural Engineering, Swiss Federal Institute of Technology (ETH) Zurich. On a jeho tým provedli rovněž verifikaci metody a její programové implementace.
Autor: Ing. Pavel Kaláb, Ph.D.,
IDEA StatiCa s.r.o.
Literatura:
[1] KAUFMANN, Walter, et al.: Compatible stress field design of structural concrete, ETH Zurich, 2020, ISBN 978-3-906916-95-8,
[2] KAUFMAN, W., MARTI, P.: Structural Concrete: Cracked Membrane Model. Journal of Structural Engineering 124 (12): 1467-75, 1998 https://doi.org/10.1061/(ASCE)0733-9445(1998)124:12(1467)
[3] KRAUS, M., M. WEBER, W. KAUFMANN, W, BOBEK, L.: Numerical analysis of experimentally tested frame corners with opening moments using the Compatible Stress Field Method (CSFM).
In: Computational Modelling of Concrete and Concrete Structures, pp. 694-03. CRC Press, 2022 https://doi.org/10.1201/9781003316404

 Compatible stress field method (CSFM) vznikla rozšířením těchto klasických teorií, umožňuje vysokou míru automatizace a je v souladu s návrhovou normou.
Compatible stress field method (CSFM) vznikla rozšířením těchto klasických teorií, umožňuje vysokou míru automatizace a je v souladu s návrhovou normou.