Analýza reakční doby při ochraně měkkých cílů v podmínkách ČR

Reakční doba osob v krizových situacích je klíčovým parametrem při stanovování celkové doby evakuace objektů. Standardní inženýrské metody posuzování objektů v rámci norem ČSN tento parametr nezohledňují. Alternativní posuzování evakuačního procesu agentními modely pohybu osob umožňují do jisté míry reprezentovat lidské chování v reakční době a přiblížit tím výstupy posouzení reálnému scénáři. Článek se zabývá analýzou reakční doby pro objekty typu měkké cíle vymezené metodikou Ministerstva vnitra ČR. Pro tyto kategorie objektů stanovuje parametry log‑normálního rozdělení reakční doby jako vstupní hodnoty pro agentní modely. Popisuje dostupné metody nastavení reakční doby v agentních modelech, které následně porovnává. Pro toto porovnání byl zpracován referenční model evakuace vzdělávacího zařízení. V rámci výsledků simulací pak byly tyto metody porovnány a byl stanoven optimální postup nastavení tohoto parametru v rámci současných možností agentních modelů.

1 ÚVOD

Jedním ze základních požadavků na moderní stavby je jejich bezpečnost. S rostoucím počtem teroristických útoků a havárií v nezabezpečených veřejných prostorech a objektech, kde se koncentruje vysoký počet osob, tzv. měkkých cílech, rostou i požadavky na minimalizaci dopadů těchto krizových událostí. Pokročilé technologie agentních modelů pohybu osob umožňují posuzovat evakuační proces měkkých cílů individuálně, a to zejména z hlediska doby evakuace a odhalení kritických míst v objektu, kde může dojít k ucpání únikových východů lidmi a v extrémním případě tragédii se ztrátami na životech způsobenou dynamikou davu. Jedním ze základních parametrů agentních modelů je reakční doba uživatelů objektu. Existuje mnoho studií a reálných incidentů, které potvrzují, že v evakuačním procesu hraje reakční doba zásadní roli. Purser a Bensilum uvádí, že při požáru v obchodním centru Woolworth v anglickém Manchesteru byl místním malířem spuštěn alarm a následně byli uživatelé centra varováni hlasovou zprávou. Na základě výpovědí svědků bylo zjištěno, že část uživatelů zareagovala na alarm a zahájila evakuaci výrazně rychleji, než jiná část (1). Při požáru objektu MGM Grand Hotel v Las Vegas v roce 1980 bylo na základě výpovědí 554 svědků zjištěno, že pouze u 8 % populace hotelu byla okamžitá evakuace první činnost po detekci požáru (2). Tyto a řada podobných incidentů potvrzují nutnost zkoumání a chápání lidského chování v reakční době pro maximální zpřesnění výsledků agentních modelů majících za cíl snížit ničivé dopady krizových událostí.

V tomto článku je představena sada analyzovaných dat reakční doby pro měkké cíle dle kategorizace Ministerstva vnitra ČR (3). Data se nepodařilo získat pro objekty typu sportovní haly a stadiony a veřejná shromáždění a průvody. Analyzovaná data budou sloužit jako vstupní parametry pro agentní model Pathfinder (4), případně jiné agentní modely. V článku je dále demonstrován vliv způsobu nastavení reakční doby na výstupy agentního modelu v rámci posouzení objektu vzdělávacího zařízení z hlediska doby evakuace. Závěrem jsou stanoveny principy, které je při určování reakční doby, jakožto vstupního parametru agentních modelů, potřeba zohlednit pro maximálně přesnou reprezentaci reálného scénáře krizové situace.

2 TEORIE REAKČNÍ DOBY

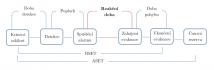
Celosvětová asociace inženýrů požární bezpečnosti definuje reakční dobu jako čas, ve kterém osoba zaznamená známky požáru a následně přijme ochranná opatření (5; 6; 1). Pro potřeby tohoto článku je tato definice zobecněna na dobu, ve které osoba rozpozná krizovou situaci vyžadující evakuaci a následně přijme ochranná opatření a zahájí evakuaci. Definice je znázorněna na obrázku 1 ¹. V případě, že osoba detekuje krizovou událost ještě před vyhlášením alarmu, je reakční doba vymezena časem detekce a zahájením evakuace. Následná doba pohybu je čas, během kterého se osoba přesune na bezpečné místo.

Lidské chování v krizových situacích popisuje E. D. Kuligowski jako soubor lidských reakcí, přístupů, motivací, přesvědčení, rozhodnutí, vlastností a schopnosti pozorování v konfrontaci s krizovou událostí v budovách či dopravních systémech (2). Jedná se o komplexní rozhodovací proces, do kterého vstupuje řada faktorů, které je potřeba při stanovování reakční doby v maximální možné míře zohlednit. Typickými příklady akcí prováděných v reakční době je získávání informací, shromažďování blízkých osob, vypínání zařízení apod. (6). Evakuační modely pracují s určitým zjednodušením oproti reálnému prostředí a vždy reprezentují konkrétní teorii lidského chování v krizových situacích, znalosti a přesvědčení vývojářů modelu. V minulosti se vývojáři modelů často zaměřovali na fyzikální aspekty pohybu a přespříliš zjednodušovali rozhodovací proces osob v krizových situacích (7).

2.1 Metody stanovování reakční doby
V požárně bezpečnostních výpočtech předpokládané doby evakuace v rámci souvisejících norem ČSN 73 0802 a 73 0831 s reakční dobou uvažováno není (8; 9). Současná absence platného komplexního postupu stanovování reakční doby umožňuje aplikovat různorodé metody při stanovování tohoto parametru. Kategoricky se dá reakční doba stanovit na základě experimentálních dat a teorií lidského chování, tedy metodami představenými v 2.1.1 a 2.1.2, nebo metodami využívajícími prediktivní modely lidského chování popsanými v 2.1.3 a 2.1.4.

2.1.1 Nastavení sekvence akcí
Reakční doba je zde stanovena uživatelem agentního modelu v podobě sekvence akcí, které agent v okamžiku spuštění alarmu vykoná. Každá tato akce má předem nadefinovanou dobu trvání (10; 11). Behaviorální akce agentů jsou tedy vstupem, nikoli výstupem modelu. Tento přístup má několik nedostatků. Uživatel má absolutní kontrolu nad sestavením akcí tvořících reakční dobu, což může vést k pokušení reakční dobu uměle redukovat ve prospěch výsledné doby evakuace. S tímto rizikem jsou spojené i vysoké nároky na zohlednění veškerých podmínek dynamiky evakuačního procesu uživatelem modelu. Takovéto nastavení reakční doby neumožňuje další analýzu výsledků simulací, vzhledem k tomu, že uživatel předepsal podmínky modelu do takové míry, že model neposkytne žádné neočekávané výsledky (7).

2.1.2 Náhodná distribuce reakční doby
Německá směrnice udávající pokyny pro tvorbu mikroskopických evakuačních analýz z roku 2016 (12) se opírá o práci Pursera (13), který na základě dostupných datových souborů stanovuje hodnoty reakční doby pro 1. a 99. percentil populace a následně ji v rozmezí těchto hodnot rovnoměrně distribuuje mezi populaci. Purser zároveň uvádí jako vhodnější metodu použití statistického rozdělení (13). Tato metoda je v pokročilých agentních modelech typu Pathfinder plně využitelná (14). Před náhodnou distribucí reakční doby varuje Kuligowski a uvádí, že nereprezentuje reálný scénář evakuačního procesu z hlediska sociologických vlivů. Pokud bychom se zaměřili např. na místnost typu kancelář, mohlo by dojít k situaci, kdy se první agent začne evakuovat a zbylí zůstanou na svých místech, dokud neuběhne jim přidělená časová hodnota reakční doby, navzdory kolegiálním sociálním vazbám (2).

2.1.3 Behaviorální prediktivní model
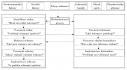
V roce 2004 představili Lindell a Perry teorii rozhodovacího modelu o ochranných opatřeních (Protective Action Decision Model – PADM), viz obrázek 2. Jedná se o teorii lidského chování a toku informací při technologických či přírodních katastrofách, mající základ v desítkách let předchozího výzkumu, studií katastrof a krizových incidentů (15). Pro implementaci PADM do evakuačních modelů je potřeba identifikovat faktory mající vliv na rozhodovací proces (11). Kuligowski tyto faktory specifikovala a představila prediktivní model reakční doby, který předpovídá ochranné akce přeživších tragédie Světového obchodního centra v roce 2001 (16). Takovýto rozhodovací model by mohl být dle Kuligowski implementován v evakuačních modelech skrze behaviorální pravidla typu „podmínka – akce“, jež agentní modely využívají (7). K implementaci obdobného prediktivního modelu v agentních modelech však zatím nedošlo.

2.1.4 Matematický prediktivní model
Jedná se např. o evakuační rozhodovací model založený na lidském vnímání rizika, sociálních vlivech a behaviorální nejistotě (dále EDM) od autorů Lovreglia, Ronchiho a Nilssona (10) mající základ na evakuačním rozhodovacím modelu Renekeho (17). Oba tyto modely se opírají v oblasti teorie lidského chování o kvalitativní model E. D. Kuligowski popsaný v 2.1.3. EDM reaguje na nedostatky metod uvedených v 2.1.1 a 2.1.2, které, mimo již zmíněné, spočívají v omezené dostupnosti datových souborů se statistickými parametry reakční doby a nedostatečném zohlednění dalších faktorů jako je např. kulturně‑sociální a demografický kontext implementovaných dat. EDM diferenciálními rovnicemi stanovuje míru vnímání rizika pro každého jednoho agenta s ohledem na sociální, environmentální, demografické podmínky, charakteristiky agenta a behaviorální nejistotu. Na základě těchto výpočtů odhaduje reakci agentů v rámci třech módů chování: normálního, investigativního a evakuačního. Jednotlivé výsledky pak v souhrnu predikují reakční dobu. EDM zajišťuje, že chování lidí v reakční době je nikoli vstupem zadávaným uživatelem, ale výstupem tohoto modelu (10). Tento a jemu podobné matematické modely však nejsou v současné době implementovány v numerických evakuačních modelech a neexistuje dostatečné množství dat, které by umožňovaly kalibraci ² těchto modelů, což jejich aplikaci komplikuje.

Vývoj v oblasti predikce lidského chování by měl na základě uvedených skutečností dále směřovat k implementaci prediktivních modelů lidského chování do evakuačních modelů. Tato inovace by umožnila kvalitnější validaci ³ modelu méně závislou na množství a validitě uživatelských vstupů a zohledňující okrajové podmínky daného scénáře při určování reakční doby.

2.2 Statistické vlastnosti reakční doby
Na základě výzkumů v oblasti lidského chování v krizových situacích realizovaných v posledních desetiletích lze konstatovat, že reakční doba může být z hlediska statistiky charakterizována jako spojitá veličina s Weibullovým, normálním nebo logaritmicko‑normálním (dále LN) rozdělením (6; 1; 18). Dle Pursera a Bensila se ve většině případů jedná o LN rozdělení, které říká, že se minoritní část populace začne evakuovat s výrazně větším zpožděním než majoritní část (1). Na základě těchto poznatků a faktu, že v agentním modelu Pathfinder lze dle LN rozdělení náhodně distribuovat reakční dobu mezi populaci, se článek dále zaměřuje právě na toto rozdělení. Hustota pravděpodobnosti (Probability Density Function – PDF) a distribuční funkce (Cumulative Distribution Function – CDF) log‑normálního rozdělení jsou popsány následujícími rovnicemi s parametry střední hodnoty μ a směrodatné odchylky σ:



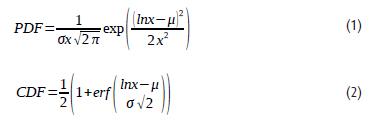
Řada publikací uvádí experimentální data o reakční době pouze formou střední hodnoty E[X] a rozptylu Var[X]. Parametry μ a σ je v těchto případech možné vyjádřit z následujících rovnic:



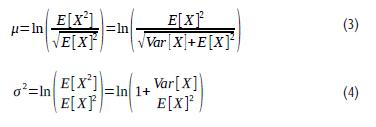
3 ANALÝZA DATOVÝCH SETŮ

V současnosti je v agentním modelu Pathfinder možné reakční dobu stanovovat pomocí sekvence akcí (viz 2.1.1) nebo náhodné distribuce reakční doby (viz 2.1.2). V rámci těchto možností byla využita rozsáhlá databáze, ve které jsou analyzovány datové sety reakční doby. Datové sety jsou sestaveny dle předem definovaných kritérií a pomocí shlukové analýzy jsou rozděleny do skupin, v rámci nichž jsou následně stanoveny parametry LN rozdělení (19). Na základě této databáze byly z grafů hustot LN rozdělení následně odečteny hodnoty reakční doby pro 1. a 99. percentil dané populace. Data jsou popsána a rozšířena o další datové sety v tabulce 1. Data se nepodařilo získat pro měkké cíle typu sportovní stadion, sportovní hala, veřejná shromáždění a průvody. Datové sety jsou roztříděny z hlediska charakteru evakuace. Jedná se o ohlášené cvičení (OC), neohlášené cvičení (NC), částečně ohlášené cvičení (ČOC) a požár (P). Zároveň byl rozlišován způsob vyhlášení evakuace – vyzváněním alarmu (A), hromadnou hlasovou zprávu (H), personálem objektu (P) a puštěním předehrané hlasové zprávy (N).

4 POROVNÁNÍ METOD STANOVENÍ REAKČNÍ DOBY V AGENTNÍM MODELU

Pro porovnání metod stanovení reakční doby byl v agentním modelu Pathfinder vytvořen evakuační model části vzdělávacího zařízení, konkrétně 4. patra budovy B, Fakulty stavební VUT v Brně, viz obrázek 3. Na tomto referenčním modelu byla testována nastavení reakční doby pomocí nastavení sekvence akcí a náhodné distribuce reakční doby. Následně byl na výsledcích simulací demonstrován vliv metody nastavení parametru na tyto výsledky.

Posuzovaný objekt je součástí budovy vysoké školy a skládá se ze 7 učeben a 16 kanceláří propojených společnou chodbou. 5 ze 7 učeben je kompletně vybaveno počítači. Z objektu vede jediná úniková cesta po dvouramenném schodišti do nižších podlaží a následně na volné prostranství. Chodba je v místě schodiště opatřena 3 bezpečnostními mřížemi, jejichž vliv na evakuační proces je popsán v 4.3. Referenční model se vztahuje pouze na 4. patro objektu a evakuace je v modelu ukončena na chodbě ve 3. patře. Objekt je opatřen výtahem, který však neslouží k evakuaci. Model počítá s maximální obsazeností objektu, která činí 299 osob (278 studentů a 21 učitelů). Procesy validace a verifikace ⁴ agentního modelu popisuje dokument (22), v němž byly provedeny testy, které potvrzují, že agentní model Pathfinder pracuje v souladu s technickou referencí softwaru (4) a vyjadřují nakolik přesně agentní model reprezentuje reálné prostředí. Základní parametry modelu jsou popsány tabulce 2.

4.1 Aplikace metody stanovení sekvence akcí
Toto nastavení parametrů reakční doby se řídí kapitolou 2.1.1. a jako podklad zde byla použita studie neohlášené cvičné evakuace knihovny na VŠB v Ostravě (27; 28). Studie měla za cíl formou analýzy videozáznamů a dotazníků vyhodnotit chování osob po vyhlášení evakuace.

Vyhodnocení proběhlo na vzorku 47 osob. Evakuace byla vyhlášena ústně personálem knihovny. Studie byla zpracována na území ČR, čímž z hlediska kulturního kontextu, na jehož význam upozorňuje Galea (27), tvoří vhodný podklad pro tuto metodu parametrizace modelu vzdělávacího zařízení. Sekvence činností prováděných neprodleně po vyhlášení evakuace Galea rozdělil na úkonové činnosti AT (Action Tasks) a informační činnosti IT (Information Tasks) s celkovým počtem 256 záznamů činností a každé z nich přiřadil poměrné zastoupení v populaci (28). Tyto činnosti jsou reprezentovány a v daných poměrech implementovány v populaci modelu dle tabulky 3. Časové hodnoty byly rovnoměrně rozděleny v daném rozmezí tak, aby se maximální doba reakční doby pohybovala v rozmezí reálné doby 80 – 100 sekund. Trajektorie pohybu byly předepsány manuálně.

4.2 Aplikace metody náhodné distribuce
Pro tuto metodu nastavení byly použity parametry LN rozdělení z tabulky 1 pro objekt typu univerzitní knihovna (μ = 4,185, σ = 0,479). Distribuce reakční doby je v zájmu porovnatelnosti s předchozí metodou nastaven na maximální hodnotu 100 s, dle reálně naměřených hodnot v objektu typu univerzitní knihovna (27).

4.3 Výsledky
V rámci každé metody bylo realizováno 100 simulací evakuačního procesu. Výsledky byly porovnány z hlediska celkové doby evakuace. Na obrázku 4 je znázorněn evakuační proces v rámci každé metody v čase 50 s. U metody náhodné distribuce, kde agenti čekají na přidělenou dobu evakuace, je názorné chování bez sociálních vazeb, jak ho popsala Kuligowski (2). Rysy rozhodovacího procesu jsou patrné u varianty nastavení sekvence akcí, kde je vidět shlukování agentů a pohyb v rámci třídy (např. k oknům). Na základě grafů na obrázku 5 bylo pro vyhodnocení výsledků použito normální rozdělení.

Charakteristiky rozdělení a kvantily p₉₅ popisuje tabulka 4. Rozdíl kvantilů p₉₅ obou metod činí 30 sekund při stejné maximální hodnotě reakční doby 100 sekund.

Graf na obrázku 6 popisuje závislost počtu lidí v objektu na čase během evakuace. Z grafu je patrný podobný průběh obou křivek. Počáteční nárůst počtu osob je zapříčiněn příchodem 20 osob z 5. patra objektu do modelu (4. patra) na počátku evakuace. Průběh evakuace má v obou metodách po většinu času téměř lineární charakter se zlomem v čase přibližně 260 s, kdy se zbytek populace evakuoval skrze jedinou bránu na chodbě objektu, což vlivem kongesce celkový čas značně navýšilo.

Použití metody nastavení sekvence akcí se jeví jako vhodné v situaci, kdy máme k dispozici detailní studii evakuace s popisem jednotlivých akcí v rámci populace stejného typu měkkého cíle a jsme tedy schopni v rámci populace reprezentovat jednotlivé činnosti v reakční době. Máme‑li k dispozici takovýto podklad, je částečně vyvráceno úskalí metody popsané v 2.1.1 v podobě možné tendence uživatele modelu výsledky uměle ovlivnit nepřesně zvoleným nastavením patřičných akcí. I zde však bylo potřeba akce typu získávání či výměna informací přenést do jazyka modelu, což může v praxi vést k umělému ovlivnění výsledků nevhodnou reprezentací těchto akcí v modelu.

Takto detailní studie chování osob v evakuačním procesu nejsou v současnosti k dispozici pro většinu typů měkkých cílů. V těchto případech je nutné použít druhou z metod, tedy náhodnou distribuci reakční doby. Tato metoda je silně závislá na validitě parametrů daného rozdělení konkrétního datového setu. Je potřeba použít datový set, který nejvíce odpovídá posuzovanému typu měkkého cíle především z hlediska typologie objektu, způsobu vyhlášení evakuace v daném objektu, počtu osob, případně lokality. Dále by měl být upřednostněn datový set, jehož data vychází z reálné krizové situace vzhledem k pravděpodobnějšímu napodobení reálného scénáře. Experiment prokázal, že užití metody náhodné distribuce reakční doby má oproti metodě nastavení sekvence akcí horší výsledky (vyšší celkovou dobu evakuace). Její použití se tedy na základě tohoto experimentu jeví jako bezpečnější varianta stanovení tohoto parametru.

5 ZÁVĚR

Pro kvalitní posuzování měkkých cílů agentními modely z hlediska doby evakuace je reakční doba klíčovým a v současnosti obtížně popsatelným parametrem, který má však zásadní vliv na výsledky těchto modelů. Řadu faktorů majících vliv na reakční dobu osob, nelze v modelech plně reprezentovat (např. rozdílná míra vnímání rizika nebo sociální vazby). Současné modely umožňují zohlednit jen omezené množství faktorů reakční doby a ve velmi omezené míře. V článku byly popsány dostupné metody stanovování reakční doby v agentních modelech. Bylo konstatováno, že vývoj v oblasti agentního modelování pohybu osob by měl směřovat k implementaci prediktivních modelů, které by zajistily zohlednění většího množství faktorů majících vliv na reakční dobu osob (viz obrázek 2) a které by na základě těchto faktorů rozhodovací proces osob v reakční době predikovaly. V článku byly analyzovány datové sety s LN rozdělením reakční doby pro jednotlivé typy měkkých cílů, které mají sloužit jako vstupní parametry v agentních modelech při zadávání metodou náhodné distribuce.

Byl proveden experiment, který demonstroval užití možných dvou metod stanovení reakční doby v agentním modelu Pathfinder a obě metody porovnal. Pro metodu stanovení reakční doby pomocí sekvence akcí byla k dispozici detailní studie evakuace univerzitní knihovny v ČR, na základě které mohl být model nastaven tak, aby agenti napodobovali rozhodovací proces a časovou hodnotu reakční doby nahradili kombinacemi akcí. Druhá z metod zahrnovala náhodnou distribuci reakční doby v rámci LN rozdělení pro měkký cíl typu univerzitní knihovna. Výsledky ukázaly, že při stejné horní hranici reakční doby 100 sekund se celková doba evakuace u metody náhodné distribuce navýšila o 30 sekund oproti metodě nastavení sekvence akcí. V rámci tohoto experimentu poskytla metoda náhodné distribuce reakční doby vyšší výslednou hodnotu celkové doby evakuace a prokázala se tedy jako bezpečnější varianta zadání tohoto parametru v agentním modelu Pathfinder.

PODĚKOVÁNÍ
Článek vznikl za podpory projektu specifického výzkumu FAST‑J‑19‑6094 Analýza reakční doby při ochranně měkkých cílů v podmínkách ČR. Poděkování patří také Oddělení krizového řízení Odboru bezpečnostního Ministerstva dopravy ČR za spolupráci na řešené problematice.

Ing. Ondřej Uhlík
Vysoké učení technické v Brně
Fakulta stavební

RECENZE
Článek Analýza reakční doby při ochraně měkkých cílů v podmínkách ČR se zabývá reakční dobou jako klíčovým parametrem při stanovování celkové doby evakuace objektů. V případě ochrany měkkých cílů musíme k analýze jejich odolnosti přistupovat jiným způsobem, než jaký nabízí standardní inženýrské metody definované soustavou norem ČSN. Posuzovaný text správně přináší nový pohled na tuto problematiku a na základě dostupných dat o reakční době osob navrhuje postup její implementace do agentních modelů. 

doc. Ing. Martin Hromada, Ph.D.
Ústav bezpečnostního inženýrství
Fakulta aplikované informatiky
Univerzita Tomáše Bati ve Zlíně

REFERENCE:
[1] Purser, D. A. a M. Bensilum. Quantification of behaviour for engineering design standards and escape time calculations. Safety Science. 2001, 38, str. 162. DOI: 10.1016/S0925‑7535(00)00066‑7
[2] Kuligowski, E. D. Human Behavior in Fire. SFPE Handbook of Fire Protection Engineering. 2016. DOI: 10.1007/978‑1‑4939‑2565‑0_58
[3] Institute of Soft Targets Protection. Základy ochrany měkkých cílů. Praha: Ministerstvo vnitra ČR. 2016.
[4] Thunderhead Engineering. Technical Reference – Pathfinder 2018 Thunderhead Engineering. 2018.
[5] Biller, J. a S. Dryden. Guide to Human Behavior in Fire, 2nd Edition NY: Springer. 2017. ISBN 978‑3‑319‑94697‑9
[6] Purser, A. D. a M. Bensilum. Grid Flow: An Object‑oriented Building Evacuation Model Combining Pre‑movement And Movement Behaviours For Performance‑based Design. Fire Safety Science. 2003. DOI: 10.3801/IAFSS.FSS.7‑941
[7] Gwynne, S. M. V., L. M. Hulse a M. J. Kinsey. Guidance for the Model Developer on Representing Human Behavior in Egress Models. Fire Technology. 2015, 52. DOI: https://doi.org/10.1007/s10694‑015‑0501‑2
[8] ČSN 73 0802,. Požární bezpečnost staveb – Nevýrobní objekty. Praha: Úřad pro technickou normalizaci, metrologii a státní zkušebnictví. 2009.
[9] ČSN 73 0831. Požární bezpečnost staveb – Shromažďovací prostory. Praha: Úřad pro technickou normalizaci, metrologii a státní zkušebnictví. 2011.
[10] Lovreglio, R., D. Nilsson, E. Ronchi. An Evacuation Decision Model based on perceived risk, social influence and beahvioural uncertainty. Simulation Modelling Practise And Theory. 2016. DOI: 10.1016/j.simpat.2016.03.006
[11] Kuligowski, E. D. Predicting Human Behaviour during Fires. Fire Technology. 2011, 49. DOI: 10.1007/s10694‑011‑0245‑6 
[12] Richtlinie für Mikroskopische Entfluchtungs‑Analysen. RiMEA e.V., 2016.
[13] Purser, A. D. Behaviour and Travel Interactions in Emergency Situations And Data Needs for Engineering Design. Second International Conference In Pedestrian And Evacuation Dynamics. University of Greenwich UK. 2003.
[14] Thunderhead Engineering. User Manual – Pathfinder 2018. Thunderhead Engineering. 2018.
[15] Lindell, K. M. a W. R. Perry. Communicating Environmental Risk in Multiethnic Communities. SAGE Publications. 2004. ISBN‑10: 0761906517
[16] Kuligowski, E. D. Terror Defeated: Occupant Sensemaking, Decision‑Making and Protective Action in the 2001 World Trade Center Disaster. University of Colorado. 2011.
Dostupné z: https://core.ac.uk/download/pdf/54848635.pdf
[17] Reneke, A. P. Evacuation Decision Model. National Institut of Standards and Technology. U.S. Department of Commerce. 2013.
[18] Spearpoint, M. The Effect of Pre‑evacuation on Evacuation Times in the Simulex Model. Journal of Fire Protection Engineering. 2004. DOI: 10.1177/1042391504034742
[19] Lovreglio, R., E. D. Kuligowski, S. M. V. Gwynne a další. A Pre-Evacuation Database for Use in Egress Simulations. Fire Safety Journal. 2019. DOI: 10.1016/j.firesaf.2018.12.009
[20] Gwynne, S. M. V., E. R. Galea, J. Parke a J, Hickson. The collection of pre‑evacuation times from evacuation trials involving a Hospital Outpatient area and a University Library facility. Fire Safety Science. 2003. DOI: 10.3801/IAFSS.FSS.7‑877
[21] Rinne, T., K. Tillander a P. Grönberg. Data collection and analysis of evacuation situations. Helsinki. 2010. ISBN 978‑951‑38‑7673‑9.

¹ Oficiální příručka požární ochrany SFPE zavádí termín doby potřebné pro evakuaci (Required Safe Egress Time – RSET) a doby dostupné pro evakuaci (Available Safe Egress Time – ASET). Obecně platí, že je zajištěna bezpečnost uživatelů, je‑li RSET menší než ASET (29).
² Proces korekce parametrů modelu s cílem dosáhnout maximální shody modelu s experimentálními daty (31).
³ Proces stanovení, nakolik je metoda výpočtu přesnou reprezentací reálného světa (31).
⁴ Proces ověření, že implementace metody výpočtu přesně odpovídá koncepčnímu popisu výpočtu vývojářů modelu (31)